斜率优化相关 - 洛谷保存站

#### **一个重要点**

设$k$为直线的斜率。

则斜率优化中的成为“决策点”（即被选做用来转移的点）的点，一定满足如下条件：

- 假设这个点为$P_0(x_i,y_i)$，设凸壳上前一个点为$P_1(x_{i-1},y_{i-1})$，后一个点为$P_2(x_{i+1},y_{i+1})$，则：

$$
k_{P_0P_1}\le k \le k_{P_1P_2}
$$

**证明：**

1. 如果：

$$
k_{P_0P_1}<k_{P_1P_2}< k
$$

则会出现此图：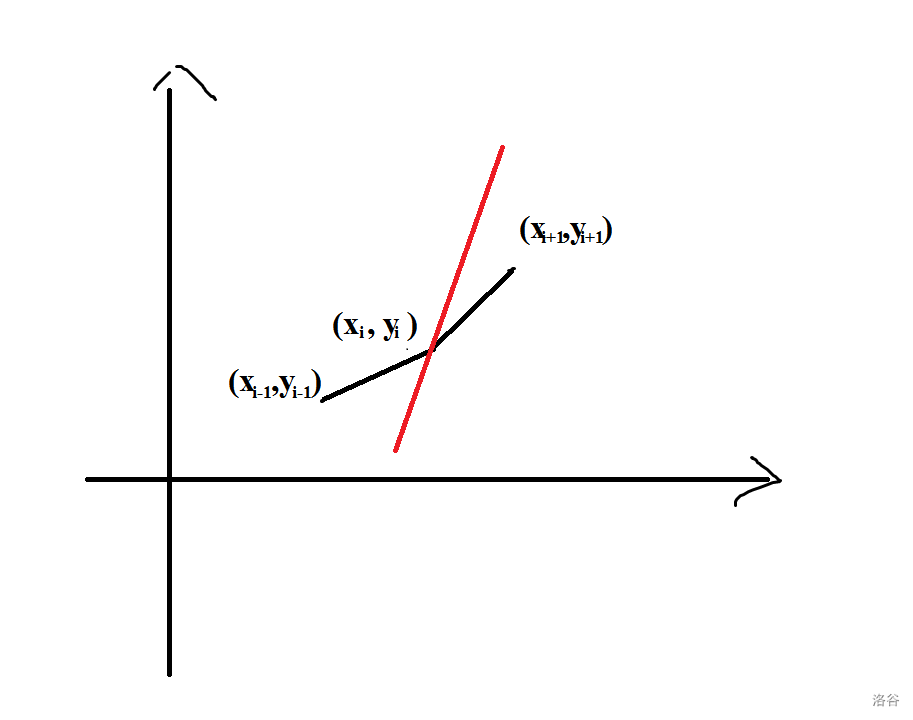

![](https://cdn.luogu.com.cn/upload/image_hosting/maipevds.png)

这样，显然点$P_2(x_{i+1},y_{i+1})$在直线的下方，将直线下移就会与  $P_2(x_{i+1},y_{i+1})$相交，$\therefore$点$P_1(x_i,y_i)$不是"决策点"。

2. 如果：

$$
k < k_{P_0P_1}<k_{P_1P_2}
$$

则会出现此图：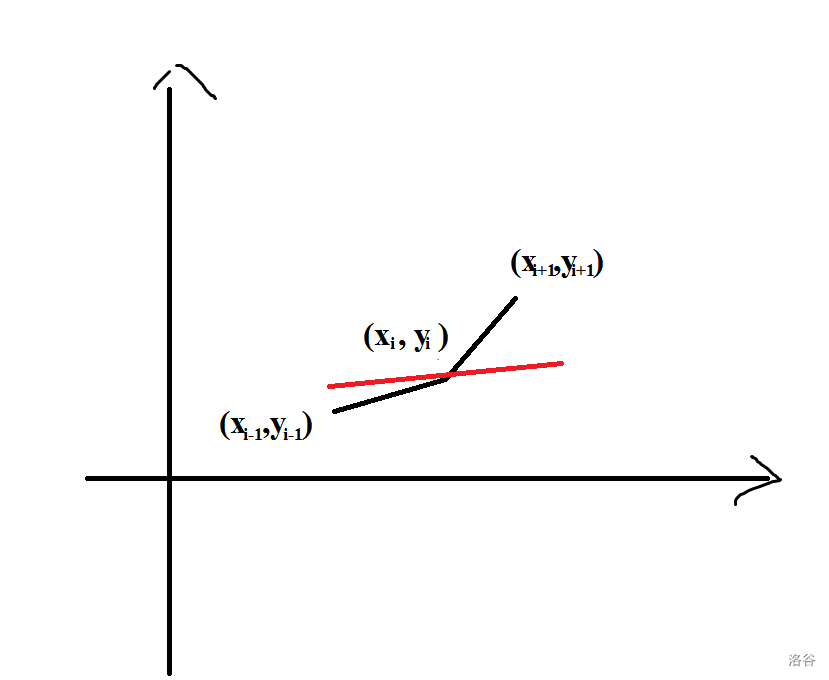

![](https://cdn.luogu.com.cn/upload/image_hosting/a5hh6el0.png)

这样，显然点$P_0(x_{i-1},y_{i-1})$在直线的下方，将直线下移就会与  $P_0(x_{i-1},y_{i-1})$相交，$\therefore$点$P_1(x_i,y_i)$不是"决策点"。

3. 所以，唯有：
   $$
   k_{P_0P_1}\le k \le k_{P_1P_2}
   $$
   如图：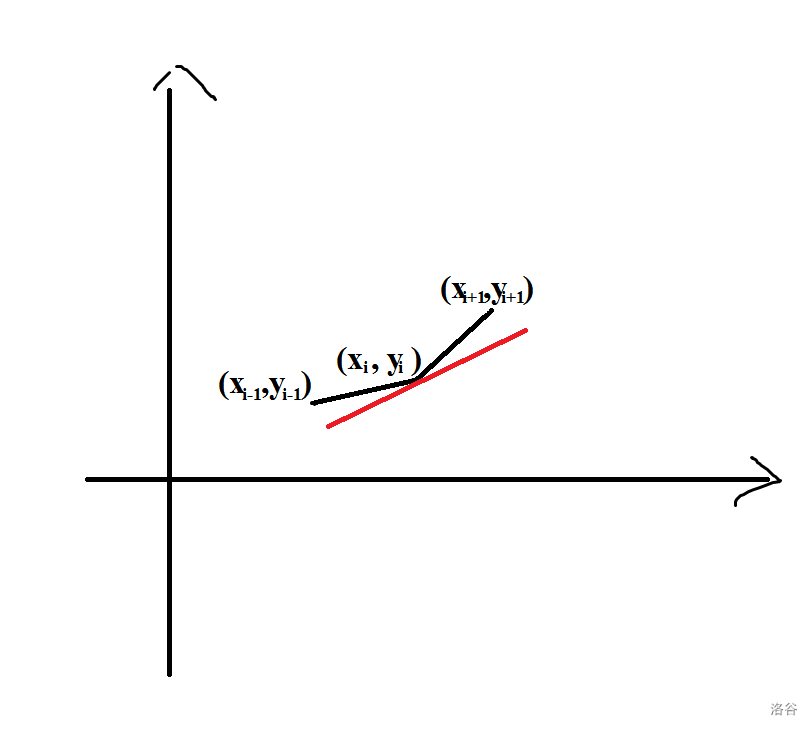

![](https://cdn.luogu.com.cn/upload/image_hosting/c86t22gj.png)

$P_1(x_i,y_i)$才会是决策点。

也就是说，对于比当前点$P$更**高**更**左**的点$Q$，若直线的斜率$k$**大于**当前点$P$与点$Q$之间的连线斜率$k_{PQ}$。以点$P$当做原点，对于同一$x$，$\because x>0$，$\therefore kx>k_{PQ}x$，即直线高于点$Q$。

对于比当前点$P$更**低**更**右**的点$Q$，若直线的斜率$k$**小于**$Q$与$P$的连线斜率$k_{QP}$。以点$P$作为原点，对于同一$x$，$\because x<0$，$\therefore kx>k_{QP}x$，即直线高于点$Q$。

由此可见，只有在斜率$k$大于比当前点更**低**更**右**的点之间连线的斜率，小于比当前点更**高**更**右**的点之间连线的斜率，才能使当前点为**”决策点“**。

所以有：
$$
k_{P_0P_1}\le k \le k_{P_1P_2}
$$

正在渲染内容...