无向图 Tarjan 割点与点双

# 省流
求割点
1. 不用维护栈，**也就没有 vis 判据**，需要维护根和 $ch$
2. 内部求割点
3. 求割点的判据是**low[v]>dfn[x]**
4. 对于非根节点，只需要一个儿子满足判据
5. 特判根节点，需要至少两个儿子满足判据

求点双

1. 访问过的点塞栈里，但是用来记录 vdcc 的，没有**vis 判据**。
2.  内部求 vdcc
3.  不需要维护根和 ch，也就是说没有特判
4.  求 vdcc 的时候，从栈中记录元素**直到 v 出栈**。最后**记录 u 但不让 u 出栈**。

# Tarjan 求割点
题目链接：[割点模板](https://www.luogu.com.cn/problem/P3388)

核心思想：主要是维护两个数组：时间戳 $dfn$ 和追溯戳 $low$。**时间戳维护第一次到某个点的时间，追溯戳维护某个点能返回到的时间戳最早的点。** 考虑如何判断一个点是不是割点：递推随着搜索深度增加而增大，对于节点 $u$，**如果它的所有子节点通过连边，顶多也只能回到 $u$，说明如果把 $u$ 删掉，它的孩子们和它上方的图无法连通**，代码体现为：

$$\min(low_1,low_2,low_3……low_v)\geq dfn_u$$

---------

给出一个样例：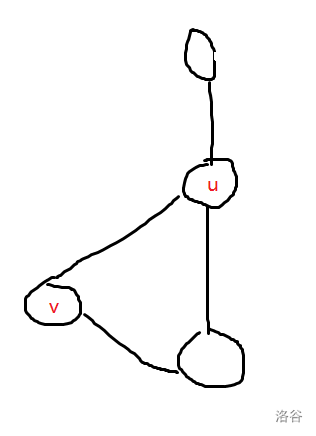

![](https://cdn.luogu.com.cn/upload/image_hosting/sj91gpkb.png)

在如上图的样例中，我们发现 $v$ 可以返回的最早的就是 $u$，而如果以 $u$ 为根的子图内没有能返回到比 $u$ 更浅的点，割掉 $u$ 肯定会导致不连通。只有子图内的点能返回到更浅的点，才能说明这个点割掉后原图依然连通。

值得注意的是：对于根节点，判断其是不是割点的依据是有没有至少两个的子节点满足上述条件。即：如果这个点有至少两个点都至多只能回到自己，于是这个点是这些环的交点，画个图，发现显然是割点。

代码实现：

1. 在一个点被搜到时，更新它的 $dfn$ 和 $low$。
2. 继续搜索它和它相邻的所有点。分两种情况：搜到搜过的，更新 $low_u=\min(low_u,dfn_v)$；或者搜到没搜过的，因为直接相连所以 $low_u=\min(low_u,low_v)$。需要注意相邻点包括父节点，这里和求割边有区别的。
3. 搜索完后，比较 $\min(low_v)$ 与 $dfn_u$，用上文的办法判断 $u$ 是不是割点。

## 代码如下
注意图可能不联通哦~

```cpp
#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int res=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9'){
		res=(res<<3)+(res<<1)+c-'0';
		c=getchar();
	}
	return res*f;
}
const int N=1e5+5;
int n,m;
int dfn[N],low[N],cut[N],tot,rt;
vector<int> e[N]; 
void tarjan(int u){
	dfn[u]=low[u]=++tot;
	int ch=0;//用于判断根节点是不是割点
	for(int i=0;i<e[u].size();i++){
		int v=e[u][i];
		if(dfn[v]==0){//未访问 
			tarjan(v);
			//回溯时更新low，判断割点
			low[u]=min(low[u],low[v]);//传递最早点
			if(low[v]>=dfn[u]){//可以回到更早的点
				ch++;
				if(u!=rt) cut[u]=1;//判断非根节点 
				else if(ch>1) cut[u]=1;//判断根节点 
			} 
		}else{//访问过 
			low[u]=min(low[u],dfn[v]);//直接找到最早点
		} 
	}
}
signed main(){
	n=read(),m=read();
	for(int i=1;i<=m;i++){
		int a=read(),b=read();
		e[a].push_back(b);
		e[b].push_back(a);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			rt=i;
			tarjan(i);
		}
	}
	int ans=0;
	for(int i=1;i<=n;i++)
		if(cut[i]) ans++;
	cout<<ans<<endl;
	for(int i=1;i<=n;i++){
		if(cut[i]) cout<<i<<" ";
	}
	return 0;
}
```

# Tarjan 求点双连通分量
题目链接：[求点双连通分量模板](https://www.luogu.com.cn/problem/P8435)

在用 tarjan 求割点时，我们用一个栈存点，若搜完了 $u$ 的一个子图，遍历返回到 $u$ 时，判定出来 $low_v\geq dfn_u$，即 $u$ 是割点，则一直从栈里弹出元素直到弹出 $v$。所有弹出来的节点和 $u$ 连在一起成为一个 vDCC。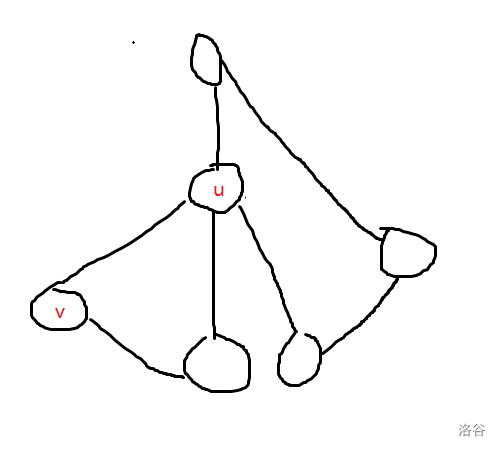

![](https://cdn.luogu.com.cn/upload/image_hosting/j5eecl9u.png)
可以参照此样例进行理解。

注意事项：

1. 一个割点可以从属于多个 vDCC，**出栈时不要把割点都出了。**
2. **判断割点要求分类讨论：是根节点和非根节点。而求点双连通分量只需要保证儿子节点回不到祖先节点即可，即： $low_v\geq dfn_u$。**
3. 一个点可能好几个子图都是点双。

## AC 代码：
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n,m;
vector<int> e[N],dcc[N];
int dfn[N],low[N],tot;
int cnt,rt,cut[N];
stack<int> st;
void tarjan(int u){
	dfn[u]=low[u]=++tot;
	st.push(u);
	if(e[u].size()==0){//特判孤立点 
		dcc[++cnt].push_back(u);
		return;
	}
	for(int i=0;i<e[u].size();i++){//割点模板 
		int v=e[u][i];
		if(!dfn[v]){
			tarjan(v);
			low[u]=min(low[u],low[v]);
			if(low[v]>=dfn[u]){
				cnt++;//找到一个点双连通分量 
				while(1){//记录点双连通分量 
					 int z=st.top();st.pop();
					 dcc[cnt].push_back(z);
					 if(z==v) break;
				}
				dcc[cnt].push_back(u);//割点也要计入点双内 
			}
		}else{
			low[u]=min(low[u],dfn[v]);
		}
	}
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int a,b;
		cin>>a>>b;
		if(a==b) continue;//警惕自环陷阱 
		e[a].push_back(b);
		e[b].push_back(a);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			rt=i;
			tarjan(i);
		}
	}
	cout<<cnt<<endl;
	for(int i=1;i<=cnt;i++){
		cout<<dcc[i].size()<<" ";
		for(int j=0;j<dcc[i].size();j++){
			cout<<dcc[i][j]<<" ";
		}
		cout<<endl;
	}
	return 0;
} 
```

正在渲染内容...