题解：P11214 【MX-J8-T2】黑洞

点 $B = (b_1,b_2,\dots,b_n)$ 与点 $A =(a_1,a_2,\dots,a_n)$ 在同一条对角线上等价于：

> 存在一个整数 $k \ge 0$，使得对于每个 $1 \le i \le n$，都有 $|a_i-b_i|=k$。

显然点 $B$ 如果合法，那么这个 $k$ 是唯一的。我们不妨枚举 $k$ 然后统计有多少个合法点 $B$。

形式化的，我们令 $c_i$ 表示有多少合法点 $B$ 对应 $k = i$。答案显然为 $\sum c_i$。现在考虑一个朴素做法，即枚举 $k$ 并计算 $c_k$ 的值。

拆绝对值。$B$ 合法需要满足 $b_i \in \{a_i+k,a_i-k\}$，以及 $b_i \in [1,m]$。

显然每个维度相互独立。我们只需要依次计算第 $i$ 维的方案数（即 $b_i$ 的合法取值数，显然一定是 $\{0,1,2\}$ 之一），乘法原理即可。

这是 $\mathcal O(n^2)$ 做法。

```cpp
c[0] = 1; 		// k = 0 单独考虑 
for (int k = 1; k <= n; ++ k ) {
	int ans = 1;
	for (int i = 1; i <= n; ++ i )
		ans *= (a[i] + k <= m) + (a[i] - k >= 1);
	c[k] = ans;
}

int ans = 0;
for (int k = 0; k <= n; ++ k ) {
  ans += c[k];
}
```

考虑优化。

上面提到过，当 $k$ 固定时，$b_i$ 的合法取值数一定在 $[0, 2]$ 内。不妨从这一点入手分析。

不妨枚举 $i$，计算会对哪些 $c_k$ 产生贡献。

当 $b_i$ 合法取值数为 $0$ 时（即 $a_i+k>m \land a_i-k < 1$ 时），一定有 $c_k = 0$。而且显然当 $k$ 越大时 $a_i+k>m \land a_i-k < 1$ 越有可能发生，即满足 $c_k=0$ 的 $k$ 一定形如一个后缀。不妨求出这个后缀的起始位置，显然是 $\min_i \max(m_i-a_i,a_i-1)$。

当 $b_i$ 合法取值数为 $1$ 时，显然没有贡献。乘 $1$ 答案显然不变。

所以有贡献的答案只有在 $b_i$ 的合法取值数为 $2$ 时（即 $a_i + k \le m \land a_i-k \ge 1$）。显然合法的 $k$ 满足 $1 \le k \le \min(m_i-a_i,a_i-1)$。于是变成了一个前缀乘 $2$ 的问题。

暴力做前缀乘二的代码是这样的：

```cpp
int max_k = INF;
for (int i = 1; i <= n; ++ i ) {
	max_k = min(max_k, max(m[i] - a[i], a[i] - 1));
}

for (int i = 0; i <= max_k; ++ i ) {
	c[i] = 1;
}

for (int i = 1; i <= n; ++ i ) {
	int r = min(m[i] - a[i], a[i] - 1);
	r = min(r, max_k);
	for (int j = 1; j <= r; ++ j ) c[i] *= 2;
}
```

考虑加速这个过程。设我们最终在 $p_1,p_2,\dots,p_m$ 做了前缀乘 $2$ 的操作，且 $p_1 \le p_2 \le \dots \le p_m$。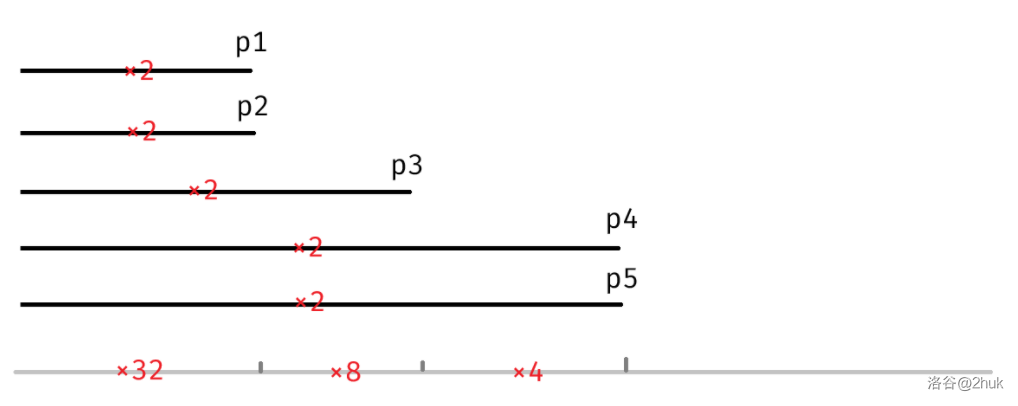

![](https://cdn.luogu.com.cn/upload/image_hosting/pav34ngv.png)

可以发现相当于对所有 $j \in (p_i,p_{i+1}]$ 执行了 $c_j \gets 2^{m-i}$。

```cpp
#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 10, P = 1e9 + 7;

typedef long long ll;
#define int ll

int n, a[N], m[N];
int res[N];

int fpm(int a, int b) {
	int res = 1;
	while (b) {
		if (b & 1) res = 1ll * res * a % P;
		b >>= 1, a = 1ll * a * a % P;
	}
	return res;
}

signed main() {
	cin >> n;
	
	for (int i = 1; i <= n; ++ i ) cin >> m[i];
	for (int i = 1; i <= n; ++ i ) cin >> a[i];
	
	int k = 1e9;
	for (int i = 1; i <= n; ++ i ) k = min(k, max(m[i] - a[i], a[i] - 1));
	
	map<int, int> mp;
	for (int i = 1; i <= n; ++ i ) {
		int l = 1, r = min(m[i] - a[i], a[i] - 1);
		r = min(r, k);
		if (l <= r) {
			mp[r] ++ ;
		}
	}
	
	mp[0] += 0, mp[k] += 0;
	
	vector<pair<int, int>> vec;
	for (auto t : mp) vec.push_back(t);
	
	int sum = 0, res = 0;
	for (int i = vec.size() - 1; i; -- i ) {
		sum += vec[i].second;
		res = (res + 1ll * (vec[i].first - vec[i - 1].first) * fpm(2, sum)) % P;
	}
	
	cout << res + 1;
	
	return 0;
}
```

正在渲染内容...