题解：P9272 [CEOI 2013] 千岛之国 / Adritic

[官方题解](https://ceoi2013.hsin.hr/tasks/tasks_and_solutions.pdf)的图：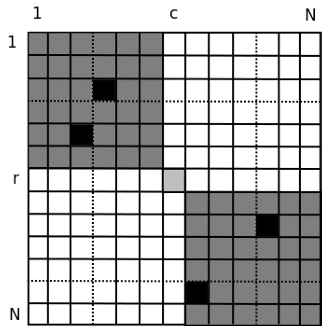

![](https://cdn.luogu.com.cn/upload/image_hosting/b5kgfb0m.png)

显然 $(r, c)$ 能一步到达的点在 **左上** 和 **右下** 这两块灰色区域。

两步能到达的点呢？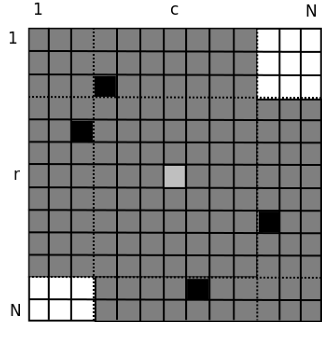

![](https://cdn.luogu.com.cn/upload/image_hosting/qhk8mogy.png)

除了 **左下** 和 **右上** 这两块白色区域内的点都可以在 $\le 2$ 步内到达。

一些尝试后可以发现，BFS 到每个阶段时，仍不能到达的点一定是一块左下区域，和一块右上区域。尝试从这一点下手。

令 $f(x,y)$ 表示若除了矩阵 $(1,y)-(x,N)$ 外，所有点都已经到达（即 BFS 过），这个矩阵内的点到**矩阵外某个点**的最短路之和。$g(x,y)$ 同理表示左下角的矩阵的答案。

那么答案为 $n-1+f(x,y)-1 + g(x,y)-1$。表示我们分别计算第一步时右上矩阵和左下矩阵的答案。为啥有三个 $-1$？因为去掉自己。

考虑怎么求 $f(x, y)$。

考虑再进行一步 BFS 后，这个白色矩阵会缩小到多少。

还是这两张图：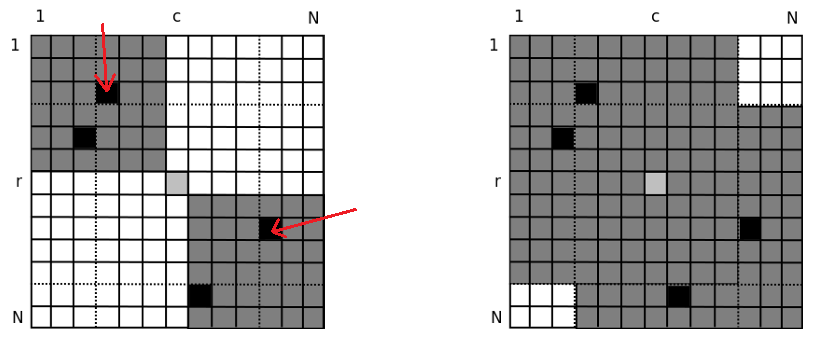

![](https://cdn.luogu.com.cn/upload/image_hosting/bjcc4nkv.png)

不难发现是箭头指的点决定了缩小后矩阵的大小。因为**新变成灰色的点都可以通过这两个点一步走到**。

而这两个点分别是什么呢？右边这个是纵坐标 $> r$ 的横坐标最大的点，上边这个是横坐标 $<c$ 的纵坐标最小的点。预处理一下就好啦。

所以 $f(x,y) = cnt(x,y)+f(x',y')$。其中 $cnt(x,y)$ 表示矩阵 $(1,y)-(x,N)$ 内的点数，$x',y'$ 表示这个新矩阵的左下角坐标。

$g(x,y)$ 同理不再赘述。

```cpp
// Problem: 
//     P9272 [CEOI 2013] 千岛之国 / Adritic
//   
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P9272
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

// #define tests
#include <bits/stdc++.h>

using namespace std;

const int N = 250010;

int n;
int a[N], b[N];
bool gra[2510][2510];
int sum[2510][2510];

int calc(int x_1, int y_1, int x_2, int y_2) {
	return sum[x_2][y_2] - sum[x_1 - 1][y_2] - sum[x_2][y_1 - 1] + sum[x_1 - 1][y_1 - 1];
}

int xmin[N];		// 横坐标 <= i 的纵坐标的最小值  1
int xmax[N];		// 横坐标 >= i 的纵坐标的最大值  3
int ymin[N];		// 纵坐标 <= i 的横坐标的最小值  4
int ymax[N];		// 纵坐标 >= i 的横坐标的最大值  2

int f[2510][2510], g[2510][2510];

int dpf(int x, int y) {
	// cout << x << ' ' << y << '\n';
	if (~f[x][y]) return f[x][y];
	
	int cnt = calc(1, y, x, 2500);
	if (!cnt) return f[x][y] = 0;
	
	f[x][y] = 0;
	return f[x][y] = cnt + dpf(min(x, xmin[y - 1]), max(y, ymax[x + 1]));
}

int dpg(int x, int y) {
	if (~g[x][y]) return g[x][y];
	
	int cnt = calc(x, 1, 2500, y);
	if (!cnt) return g[x][y] = 0;
	
	g[x][y] = 0;
	return g[x][y] = cnt + dpg(max(x, xmax[y + 1]), min(y, ymin[x - 1]));
}

void solve() {
	cin >> n;
	
	memset(xmin, 0x3f, sizeof xmin);
	memset(ymin, 0x3f, sizeof ymin);
	for (int i = 1; i <= n; ++ i ) {
		cin >> a[i] >> b[i];
		gra[a[i]][b[i]] = true;
		ymin[a[i]] = min(ymin[a[i]], b[i]);
		ymax[a[i]] = max(ymax[a[i]], b[i]);
		xmin[b[i]] = min(xmin[b[i]], a[i]);
		xmax[b[i]] = max(xmax[b[i]], a[i]);
	}
	
	for (int i = 1; i <= 2500; ++ i )
		for (int j = 1; j <= 2500; ++ j )
			sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + gra[i][j];
	
	for (int i = 1; i <= 2500; ++ i ) {
		xmin[i] = min(xmin[i], xmin[i - 1]);
		ymin[i] = min(ymin[i], ymin[i - 1]);
	}
	
	for (int i = 2500; ~i; -- i ) {
		xmax[i] = max(xmax[i], xmax[i + 1]);
		ymax[i] = max(ymax[i], ymax[i + 1]);
	}
	
	memset(f, -1, sizeof f);
	memset(g, -1, sizeof g);
	for (int i = 1; i <= n; ++ i ) {
		cout << n - 1 + dpf(a[i], b[i]) + dpg(a[i], b[i]) - 2 << '\n';
	}
}

signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	int T = 1;
#ifdef tests
	cin >> T;
#endif
	while (T -- ) solve();
	return 0;
}
```

正在渲染内容...