主页
搜索
最近更新
数据统计
申请密钥
批量保存
开发版网站(新前端)
系统公告
1
/
1
请查看完所有公告
AT_tenka1_2018_e Equilateral 题解
最后更新于 2025-08-27 19:23:41
作者
tder
分类
题解
题解
AT_tenka1_2018_e
复制 Markdown
查看原文
转到新前端
删除文章
更新内容
> You can view the [English version](https://www.luogu.com/article/oth85fqt/) of this solution. > 图片托管于 Github,若加载失败请使用加速器。 考虑画出三个点的哈夫曼距离。 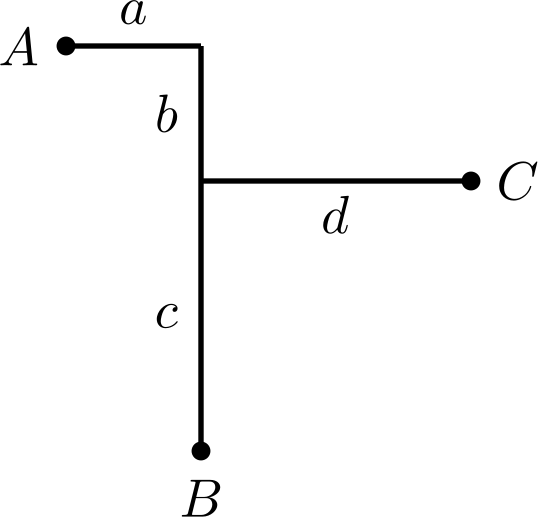 则有 $a+b+c=a+b+d=c+d$,即 $a+b=c=d$。这也就是说,$\overline{BC}$ 的斜率为 $\pm1$,而 $A$ 在与之平行的一条线上。 我们不妨 $\mathcal{O}(n^2)$ 枚举 $B$,$\mathcal{O}(n)$ 枚举 $C$,通过差分 $\mathcal{O}(1)$ 计算合法的 $A$ 的数量。复杂度 $\mathcal{O}(n^3)$,有较大常数。 具体的,我们枚举 $(i,j)$ 和 $k<i$,问题转化为求四条线上 $a_{x,y}=1$ 的个数。对每条斜率为 $\pm1$ 的直线预处理出前缀和即可。  需要注意,为了避免算重,不妨将特殊的端点位置单独计算。 [Code.](https://atcoder.jp/contests/tenka1-2018/submissions/60270468)
正在渲染内容...
点赞
1
收藏
0