【算法】折半搜索 - 洛谷保存站

教练让我们给新初一的同学讲课，然后我就抽到了折半搜索和【数据删除】。

然后就有了这篇博客。

## 折半搜索
折半搜索（双向搜索），又称 meet in the middle。

**这种搜索就是从初态和终态出发各搜索一半状态，产生两颗深度减半的搜索树，在中间交会、组合成最终的答案。**

面对一些使用dfs或bfs难以解决的题，我们可以使用折半搜索。

在一些时间复杂度为 $O(2^n)$ 的做法中，可以用折半搜索使其时间复杂度变为 $O(2\times2^{\frac n2})$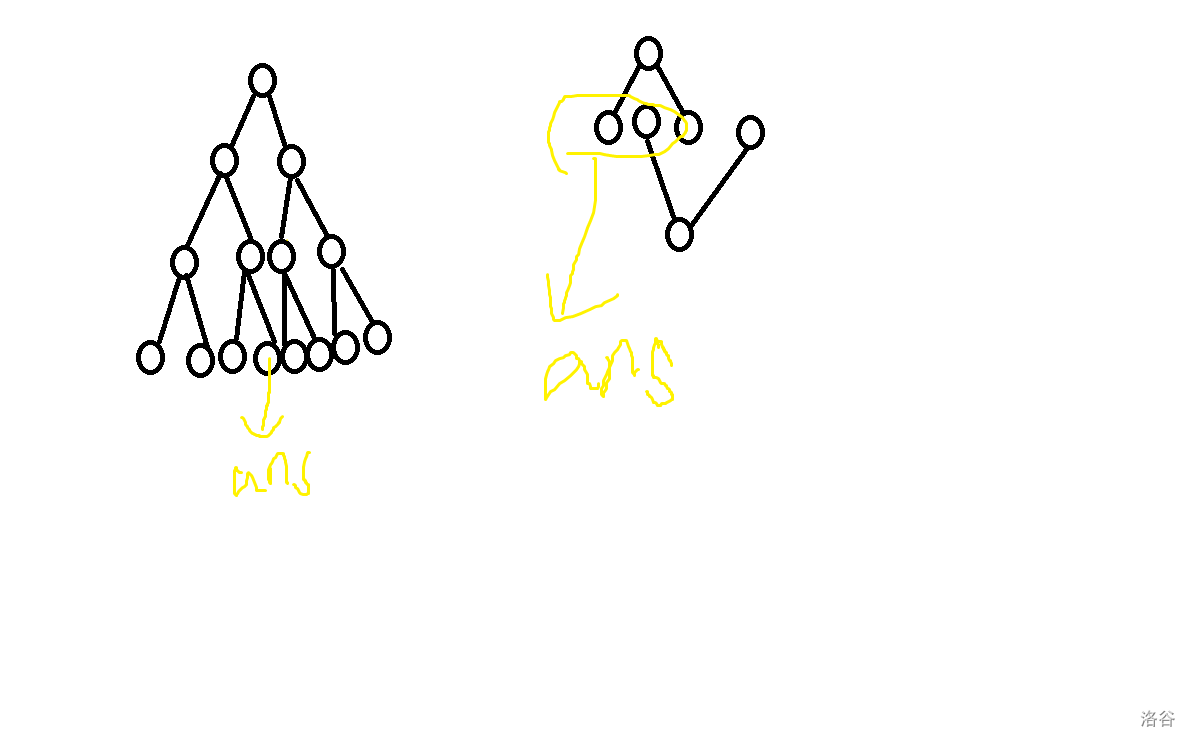

![](https://cdn.luogu.com.cn/upload/image_hosting/fy0arv4p.png)

例如这幅图，左侧是直接进行一次搜索产生的搜索树，右侧是双向搜索的两棵搜索树，显然的，双向搜索避免了层数过深时分支数量大规模增长。

注意：在很多折半搜索题目中题目中都需要用到二分，用来组合最终答案。

### 深搜

#### [P4799 [CEOI 2015] 世界冰球锦标赛 (Day2)](https://www.luogu.com.cn/problem/P4799)

一道非常经典的折半搜索题，只要求出前一半的所有可能情况和后一半的所有可能情况，二分一下即可。

code
```cpp
#include <bits/stdc++.h>
using namespace std;
long long n,m;
long long cnt1,cnt2,a[50],b[1100010],c[1100010];
void dfs1(int k,long long cur)
{
    if(cur>m) return;
    if(k==n/2+1)
    {
        b[++cnt1]=cur;
        return;
    }
    dfs1(k+1,cur);
    dfs1(k+1,cur+a[k]);
}
void dfs2(int k,long long  cur)
{
    if(cur>m) return;
    if(k==n/2)
    {
        c[++cnt2]=cur;
        return;
    }
    dfs2(k-1,cur);
    dfs2(k-1,cur+a[k]);
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    dfs1(1,0);
    dfs2(n,0);
    sort(c+1,c+cnt2+1);
    long long ans=0;
    for(int i=1;i<=cnt1;i++)
    {
        int t=upper_bound(c+1,c+cnt2+1,m-b[i])-c;
        ans+=(long long)t-1;
    }
    cout<<ans<<endl;
    return 0;
}
```

#### [P3067 [USACO12OPEN] Balanced Cow Subsets G](https://www.luogu.com.cn/problem/P3067)

这个题可以说是上一题的加强版

首先，暴搜 $O(3^n)$ 显然不行

每只奶牛只有三种情况，放A/放B/不放

设前一半放在 $A$ 组中的有 $a_1$ 个，放在 $B$ 组中的有 $b_1$ 个；后一半放在 $A$ 组中的有 $a_2$ 个，放在 $B$ 组中的有 $b_2$ 个。

依题得 $a_1+a_2=b_1+b_2$

移项得 $a_1-b_1=b_2-a_2$

统计前一半 $a_1-b_1$ 的方案，看看有没有后一半的 $b_2-a_2$ 与之相等。

折半搜索即可。

```cpp
#include <bits/stdc++.h>
using namespace std;

#define For(i,x,y,...) for(int i=(x),##__VA_ARGS__;i<=(y);++i)
#define foR(i,x,y,...) for(int i=(x),##__VA_ARGS__;i>=(y);--i)
#define Rep(i,x,y,...) for(int i=(x),##__VA_ARGS__;i<(y);++i)
#define endl '\n'
#define debug(...)
#define debug1(a,i,...) cout<<i<<" "<<a[i]<<endl;
typedef long long ll;
#define fi first
#define se second
#define PII pair<int,int>
#define me(s,x) memset(s,x,sizeof s)
#define pb emplace_back

#define LOCAL
template<typename T>ostream&operator<<(ostream&os,const vector<T>&v)
{
	os<<"[";
	for(int i=0;i<v.size();++i){os<<v[i];if(i!=v.size()-1)os<<", ";}
	os<<"]";
	return os;
}
template<typename T>ostream&operator<<(ostream&os,const set<T>&s){
	os<<"{";bool first=1;
	for(const auto&x:s){if(!first)os<<", ";os<<x;first=0;}
	os<<"}";
	return os;
}
template<typename K,typename V>ostream&operator<<(ostream&os,const map<K,V>&m){
	os<<"{";bool first=1;
	for(const auto&p:m){if(!first)os<<", ";os<<p.fi<<":"<<p.se;first=0;}
	os<<"}";
	return os;
}
template<typename A,typename B>ostream&operator<<(ostream&os,const pair<A,B>&p){
	return os<<"("<<p.fi<<", "<<p.se<<")";
}
#ifdef LOCAL
#define debug(...) cerr<<"["<<#__VA_ARGS__<<"]:",debug_out(__VA_ARGS__)
void debug_out(){cerr<<endl;}
template<typename Head,typename... Tail>
void debug_out(Head H,Tail... T){
	cerr<<" "<<H;
	debug_out(T...);
}
#else
#define debug(...) 42
#endif

template<typename T=int>T read(){T x;cin>>x;return x;}
const int mod=20140921;
struct mint{
	int x;mint(int x=0):x(x<0?x+mod:x<mod?x:x-mod){}
	mint(ll y){y%=mod,x=y<0?y+mod:y;}
	mint& operator += (const mint &y){x=x+y.x<mod?x+y.x:x+y.x-mod;return *this;}
	mint& operator -= (const mint &y){x=x<y.x?x-y.x+mod:x-y.x;return *this;}
	mint& operator *= (const mint &y){x=1ll*x*y.x%mod;return *this;}
	friend mint operator + (mint x,const mint &y){return x+y;}
	friend mint operator - (mint x,const mint &y){return x-y;}
	friend mint operator * (mint x,const mint &y){return x*y;}
};mint Pow(mint x,ll y=mod-2){mint z(1);for(;y;y>>=1,x*=x)if(y&1)z*=x;return z;}
const int N=25;
int a[N],ans;
bool vis[1<<N];
int n,tot;
map<ll,int> mp;
vector<int> v[1<<N];
void dfs1(int u,ll sum,int used){
	if(u==n/2+1){
		if(!mp.count(sum)) mp[sum]=++tot;
		v[mp[sum]].pb(used);
		return;
	}
	dfs1(u+1,sum+a[u],used|(1<<(u-1)));
	dfs1(u+1,sum-a[u],used|(1<<(u-1)));
	dfs1(u+1,sum,used);
}
void dfs2(int u,ll sum,int used){
	if(u==n/2){
		if(mp[sum]){
			for(auto x:v[mp[sum]]) if(!vis[x|used]&&x|used!=0) vis[x|used]=1,ans++;
		}
		return;
	}
	dfs2(u-1,sum+a[u],used|(1<<(u-1)));
	dfs2(u-1,sum-a[u],used|(1<<(u-1)));
	dfs2(u-1,sum,used);
}
void MAIN(){
	cin>>n;
	For(i,1,n) cin>>a[i];
	dfs1(1,0,0);dfs2(n,0,0);
	cout<<ans<<endl;
}signed main(){
	int t=1;while(t--){
		MAIN();
	}
	return 0;
}
```
于是这道蓝题就被轻松拿下了。

#### [P12878[蓝桥杯 2025 国 C] 拔河](https://www.luogu.com.cn/problem/P12878)

提答题。

考虑折半搜索，显然前一半后一半都有正或负的可能，所以枚举前一半后在后一半中二分其相反数即可。

答案为 ```**66```

#### [[ABC271F] XOR on Grid Path](https://www.luogu.com.cn/problem/AT_abc271_f)

注意到 $a \oplus a=0$，只需找前一半和后一半相同的数即可。

注意下标，及是否“包括”。

#### [CF912E Prime Gift](https://www.luogu.com.cn/problem/CF912E)

一道比较有实力的折半搜索，很好的折半搜索+二分。

这里的折半搜索有个技巧，如果我们直接分两半很容易爆long long，因此我们尽量均分两组数，可以把数组排序之后奇数和偶数进行分组。

接下来就是二分。check函数是一个双指针，$l$ 就代表 能使 $x+v2[l]<=mid$ 的最大的下标。

最后和 $k$ 比较即可。

```cpp
#include <bits/stdc++.h>
using namespace std;

template<typename T=int>T read(){T x;cin>>x;return x;}
const int mod=20140921;
struct mint{
	int x;mint(int x=0):x(x<0?x+mod:x<mod?x:x-mod){}
	mint(ll y){y%=mod,x=y<0?y+mod:y;}
	mint& operator += (const mint &y){x=x+y.x<mod?x+y.x:x+y.x-mod;return *this;}
	mint& operator -= (const mint &y){x=x<y.x?x-y.x+mod:x-y.x;return *this;}
	mint& operator *= (const mint &y){x=1ll*x*y.x%mod;return *this;}
	friend mint operator + (mint x,const mint &y){return x+y;}
	friend mint operator - (mint x,const mint &y){return x-y;}
	friend mint operator * (mint x,const mint &y){return x*y;}
};mint Pow(mint x,ll y=mod-2){mint z(1);for(;y;y>>=1,x*=x)if(y&1)z*=x;return z;}
const int N=20;
#define int unsigned long long
int p[N];
vector<int> v1,v2;
int n,k; 
void dfs1(int u,int sum){
	if(u>n){
		v1.pb(sum);
		return;
	}
	for(int i=1;;i*=1ll*p[u]){
		if(sum>1e18/i) break;
		dfs1(u+2,sum*i);
	}
}
void dfs2(int u,int sum){
	if(u>n){
		v2.pb(sum);
		return;
	}
	for(int i=1;;i*=1ll*p[u]){
		if(sum>1e18/i) break;
		dfs2(u+2,sum*i);
	}	
}
bool chk(int mid){//<=mid
	int l=v2.size()-1;
	int res=0;
	for(auto x:v1){
		if(x>mid) break;
		while(l>=0&&mid/v2[l]<x) --l;
		res+=l+1;
	}
	return res<k;
}
void MAIN(){
	cin>>n;
	For(i,1,n) cin>>p[i];
	cin>>k;
	sort(p+1,p+n+1);
	dfs1(1,1),dfs2(2,1);
	sort(v1.begin(),v1.end()),sort(v2.begin(),v2.end());
	int l=1,r=1e18,ans=0;
	while(l<=r){
		int mid=l+r>>1;
		if(chk(mid)){
			l=mid+1;
		}
		else{
			r=mid-1;
			ans=mid;
		}
	}
	cout<<ans<<endl;
}signed main(){
	int t=1;while(t--){
		MAIN();
	}
	return 0;
}
```

### 广搜

#### [P10487 Nightmare II](https://www.luogu.com.cn/problem/P10487)

一道比较有实力的bfs双向搜索。

还是比较板的

有几个需要注意的地方：

- 要保证两人 **同时** 行走。

- 男生走的时候不能只看终点，还要看路径上的点有没有鬼魂。

- 在一个点走到另一个点后，有可能到达的点上一步还没有鬼魂，下一步还没走就有了，遇到这种情况这个点就不能再走了。

4.2k代码，仅供参考（我觉得没人会愿意抄的）。

```cpp
#include <bits/stdc++.h>
using namespace std;

#define For(i,x,y,...) for(int i=(x),##__VA_ARGS__;i<=(y);++i)
#define foR(i,x,y,...) for(int i=(x),##__VA_ARGS__;i>=(y);--i)
#define Rep(i,x,y,...) for(int i=(x),##__VA_ARGS__;i<(y);++i)
#define endl '\n'
typedef long long ll;
#define fi first
#define se second
#define PII pair<int,int>
#define me(s,x) memset(s,x,sizeof s)
#define pb emplace_back

template<typename T=int>T read(){T x;cin>>x;return x;}
const int mod=1e9+7;
struct mint{
	int x;mint(int x=0):x(x<0?x+mod:x<mod?x:x-mod){}
	mint(ll y){y%=mod,x=y<0?y+mod:y;}
	mint& operator += (const mint &y){x=x+y.x<mod?x+y.x:x+y.x-mod;return *this;}
	mint& operator -= (const mint &y){x=x<y.x?x-y.x+mod:x-y.x;return *this;}
	mint& operator *= (const mint &y){x=1ll*x*y.x%mod;return *this;}
	friend mint operator + (mint x,const mint &y){return x+y;}
	friend mint operator - (mint x,const mint &y){return x-y;}
	friend mint operator * (mint x,const mint &y){return x*y;}
};mint Pow(mint x,ll y=mod-2){mint z(1);for(;y;y>>=1,x*=x)if(y&1)z*=x;return z;}
const int N=805;
char c[N][N];
bool vis1[N][N],vis2[N][N];
int n,m;
int zx1,zy1,zx2,zy2,sx1,sy1,sx2,sy2;
struct no{
	int x,y,dis;
};
int dx[]={0,1,-1,0,0},dy[]={0,0,0,1,-1};
queue<no> q1,q2;
bool in(int t,int x,int y){
	return abs(zx1-x)+abs(zy1-y)<=2*t||abs(zx2-x)+abs(zy2-y)<=2*t;
}
bool chk(int x,int y){
	return x>=1&&x<=n&&y>=1&&y<=m&&c[x][y]!='X';
}
vector<PII> v; 
int bfs(){
	q1.push({sx1,sy1,0});
	q2.push({sx2,sy2,0});
	vis1[sx1][sy1]=vis2[sx2][sy2]=1;
	while(!q1.empty()&&!q2.empty()){
		ll t=q1.front().dis;
		v.clear();
		while(!q1.empty()&&q1.front().dis==t){
			if(in(t+1,q1.front().x,q1.front().y)){
				q1.pop();continue;
			}
			v.push_back({q1.front().x,q1.front().y});
			q1.pop();
		}
		for(auto &[x,y]:v){
			For(i,0,4)For(j,0,4)For(k,0,4){
				int nx=x+dx[i]+dx[j]+dx[k],ny=y+dy[i]+dy[j]+dy[k]; 
				if(nx==x&&ny==y) continue;
				if(in(t+1,x+dx[i],y+dy[i])||in(t+1,x+dx[i]+dx[j],y+dy[i]+dy[j])||in(t+1,nx,ny)) continue; 
				if(!chk(x+dx[i],y+dy[i])||!chk(x+dx[i]+dx[j],y+dy[i]+dy[j])||!chk(nx,ny)||vis1[nx][ny]) continue;
	
				if(vis2[nx][ny]){
					return t+1;
				}
				vis1[x+dx[i]][y+dy[i]]=vis1[x+dx[i]+dx[j]][y+dy[i]+dy[j]]=vis1[nx][ny]=1;
				q1.push({nx,ny,t+1});
				vis1[nx][ny]=1;
			}
		}
		v.clear();
		while(!q2.empty()&&q2.front().dis==t){
			if(in(t+1,q2.front().x,q2.front().y)){
				q2.pop();continue;
			}
			v.push_back({q2.front().x,q2.front().y});
			q2.pop();
		}
		for(auto &[x,y]:v){
			For(i,1,4){
				int nx=x+dx[i],ny=y+dy[i];
				if(nx<1||nx>n||ny<1||ny>m||c[nx][ny]=='X'||vis2[nx][ny]||in(t+1,nx,ny)) continue;
				if(vis1[nx][ny]){
					return t+1;
				}
				q2.push({nx,ny,t+1});
				vis2[nx][ny]=1;
			}	
		}
		
	}
	return -1;
}
void MAIN(){
	zx1=0; 
	while(!q1.empty()) q1.pop();
	while(!q2.empty()) q2.pop();
	me(vis1,0),me(vis2,0);
	cin>>n>>m;
	For(i,1,n){
		For(j,1,m){
			cin>>c[i][j];
			if(c[i][j]=='Z'){
				if(!zx1) zx1=i,zy1=j;
				else zx2=i,zy2=j;
			}
			if(c[i][j]=='M') sx1=i,sy1=j;
			if(c[i][j]=='G') sx2=i,sy2=j;
		}
	}
	cout<<bfs()<<endl;
}signed main(){
	int t=read();while(t--){
		MAIN();
	}
	return 0;
}
```

#### [P2324 [SCOI2005] 骑士精神](https://www.luogu.com.cn/problem/P2324)

将矩阵转换为字符串，可以用map判重，进行双向 bfs。

在放入 $8$ 步之后，如果最后大于 $15$，就输出 ```-1```。

顺便提一句，这个题 A*、IDA* 或者 IDDFS 也很好写，有兴趣的同学可以学一下。

其实这几个算法都是互通的。

正在渲染内容...