B3694 数列离散化题解

既然题目都说了用离散化，那么自然就要用离散化去写。

### 什么是离散化？

举个例子，给出一个集合 $\{ 1,100000,999,15\}$，那么离散化后就是 $\{1,4,3,2\}$。

我想你能看出来离散化是干啥的了，那这么做的目的是什么？

比如[这道题](https://www.luogu.com.cn/problem/P1496)，如果对每一个位置都建立一个桶，那显然空间会炸，但是解决这道题只需要着火点的相对位置和它们的坐标就能解决，而求出相对位置就是离散化要干的事情。

### 如何实现离散化？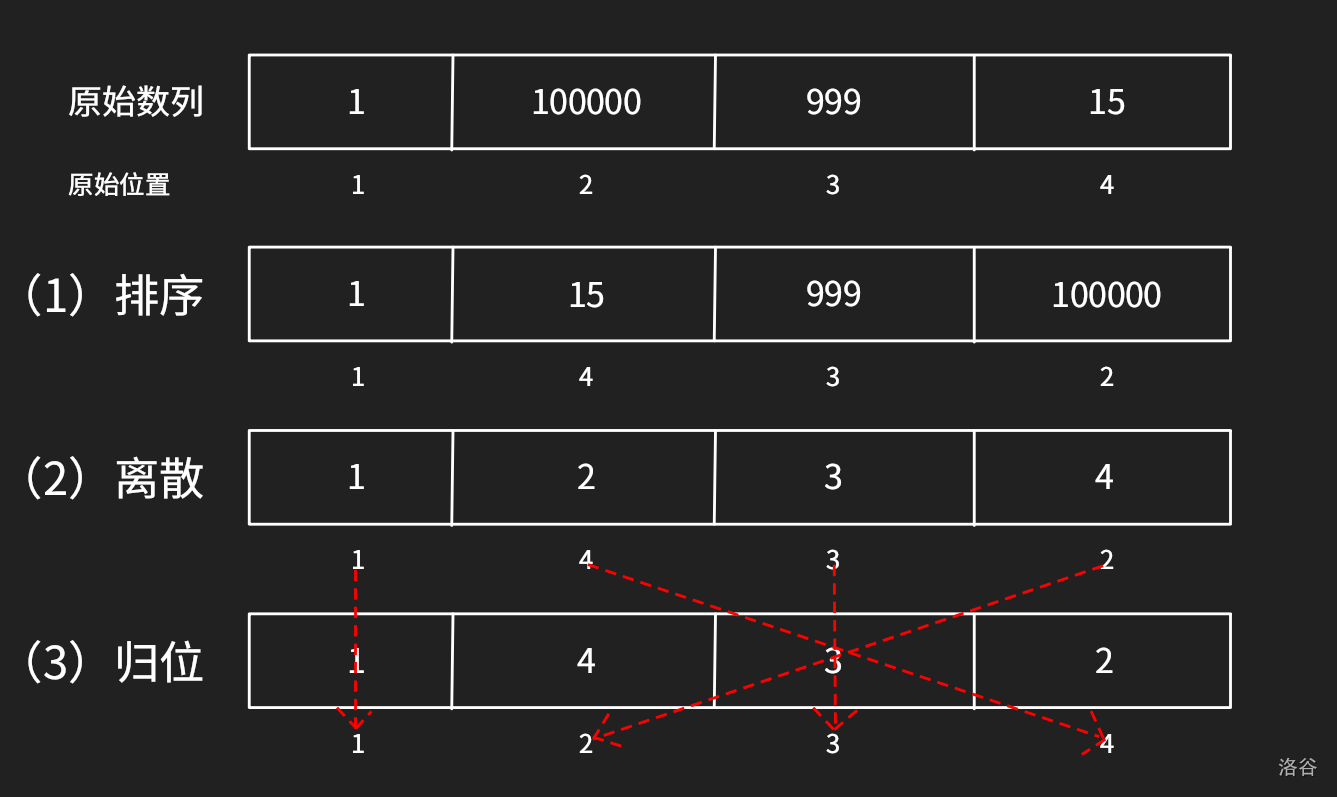

![](https://cdn.luogu.com.cn/upload/image_hosting/7mof94th.png)

我们可以发现，最后归位后的数组就对应的是 $\texttt{rank}$ 的值，因此这道题就是去求出最后的数组。

另外还需注意，题目中说“不同数字的个数”，所以本题要去重。

### 怎么用代码实现？

这道题要有两个数组，一个原数组，设为 $a$。一个离散化归位数组，设为 $d$。输入时要将原数组同步到离散化数组上。

首先对 $a$ 排序。

此时我们需要进行去重，我们可以用 STL 中的一个神奇的函数：$\texttt{unique}$，~~STL 好闪，拜谢 STL~~，使用方法跟 $\texttt{sort}$ 函数一样，只不过没有第三个参数。

注意到去重后序列元素的个数有变化，所以我们需要求它。去重后的个数会用到一行神奇的代码：```unique(a+1,a+n+1)-(a+1)```，就能求出去重的个数了。

接下来我们考虑如何归位。之前还有一个没动过的数组 $d$，现在的目标是将 $d$ 中的每一个元素在 $a$ 中找到并求出这个元素在 $a$ 从左到右第几个。注意到 $a$ 具有单调性，可以用二分实现。

你可以手写二分，但是如果你不想手写二分，可以用 $\texttt{lower\_bound}$，形式是这样的：```lower_bound(first,last,val)``` 可以查找区间中第一个**大于等于** $\texttt{val}$ 的值。```lower_bound(a+1,a+n+1,d[i])-a``` 可以返回 $a$ 中第一个大于等于 $d_i$ 的位置，输出这个结果即可。

### AC Code

```cpp
#include<iostream>
#include<algorithm>
using namespace std;
int a[100005],d[100005];//原数组和离散化数组

int main(){
	ios::sync_with_stdio(0);
	int T,n;
	cin>>T;
	while(T--){
		cin>>n;
		for(int i=1;i<=n;i++){
			cin>>a[i];
			d[i]=a[i];//同步原数组数据
		} 
		sort(a+1,a+n+1);//排序
		int cnt=unique(a+1,a+n+1)-(a+1);//去重
		for(int i=1;i<=n;i++){
			d[i]=lower_bound(a+1,a+cnt+1,d[i])-a;//归位
		}
		for(int i=1;i<=n;i++) cout<<d[i]<<" ";
		cout<<endl;
	}
	return 0;
}
```

### upd

2024.11.23：重写对于离散化概念的解释，对于如何代码实现进行进一步的说明，更加容易理解。

2025.3.17：对离散化的意义进行更详细的解释。

正在渲染内容...

B3694 数列离散化 题解

B3694 数列离散化题解