题解：P6227 [BalticOI 2019 Day1] 山谷

类似题是 [CF2033G](https://www.luogu.com.cn/problem/CF2033G)。[我的题解](https://www.luogu.com.cn/article/04w4e8nz)。这两道题思想几乎完全一样。

既然 $E$ 这个点这么特殊，不妨把 $E$ 定为这棵树的根。

断掉树边 $(fa_u, u)$ 后，$x$ **不**能到达根，等价于 $x$ 在 $u$ 的子树中，或者说 $lca(u,x)=u$。不满足这个的先判掉。

如果 $x$ 确实不能到达根，那么它能到达的点一定是 $u$ 的子树。于是问题变成了：

- 求 $u$ 的子树内，距离 $x$ 最近的 **关键点**（关键点就是题目中的商店，下同）。

这个答案有两种情况：在 $x$ 的子树内，和不在 $x$ 的子树内但在 $u$ 的子树内。对于前者，我们可以找到这颗子树内 **深度** 最小的点（这里深度指到根的边权和）。可以用 dfs 序拍到序列上然后 RMQ。

对于不在 $x$ 的子树内但在 $u$ 的子树内的情况，不妨枚举这个答案点和 $x$ 的 LCA。不妨令 $x \sim u$ 这条路径上的点分别是 $p_0,p_1,\dots,p_k$（$p_0=x,p_k=u$）。可以发现它们的 LCA 一定在 $p$ 中。

令 $f(x)$ 表示在 $\text{Subtree}(fa_u) / \text{Subtree}(u)$ 中的关键点到 $fa_x$ 的最近距离。其中 $\text{Subtree}(u)$ 表示 $u$ 所在的子树内的点的集合。

下面是一个例子，其中 $4,5$ 是关键点，$f(2)=+\infty,f(3)=4,f(4)=f(5)=0$。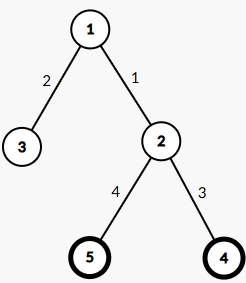

![](https://cdn.luogu.com.cn/upload/image_hosting/ipt1n512.png)

不难发现答案为 $\min f(p_{i-1}) + dis(x,p_i)$。表示 $p_i$ 是 $x$ 和答案点的 LCA。$dis(i,j)$ 表示树上 $i \sim j$ 的边权和。

先考虑 $f(u)$ 怎么求。仍然是 dfs 序。令 $u$ 的子树的 dfs 序为 $[L_u,R_u]$。那么需要求的是 $[L_{fa_u},L_u+1]$ 和 $[R_u+1,R_{fa_u}]$ 中的深度的最小值。

然后考虑 $\min f(p_{i-1}) + dis(x,p_i)$ 怎么快速求。首先这个 $dis$ 可以差分，得到 $dis(1, x) + \min f(p_{i-1})-dis(1,p_i)$。而且 $p_i$ 是 $p_{i-1}$ 的父亲。于是我们令 $g(u) = f(u) - dis(1,fa_u)$。那么答案为 $dis(1,x) + \min_{i=0}^{k-1} g(p_i)$。

那么 $\min_{i=0}^{k-1} g(p_i)$ 怎么求？倍增即可。

代码太丑了不放了。

正在渲染内容...