题解：CF2031E Penchick and Chloe's Trees

> 求最小的 $d$，使得可以在深度为 $d$ 的满二叉树上删除若干点后，与给定的树同构。
>
> 这里删掉点 $u$ 后，$u$ 的所有儿子都会连到 $u$ 的父亲上。
>
> $n \le 10^6$。

显然树形 DP 是必要的。$f(u)$ 表示 $u$ 子树的答案，即最小的合法满二叉树的深度。

如果 $u$ 是叶子（没有儿子）：$f(u)=1$；

如果 $u$ 只有一个儿子：$f(u)=f(v)+1$；

否则，考虑一个类似合并的过程。我们举几个例子。如果 $u$ 的儿子的 DP 值是：
- $[3, 3]$：$f(u)=4$；
- $[3, 3, 3, 3]$：$f(u)=5$；
- $[3, 3, 3]$：$f(u)=5$；
- $[1,3,3]$：$f(u)=5$；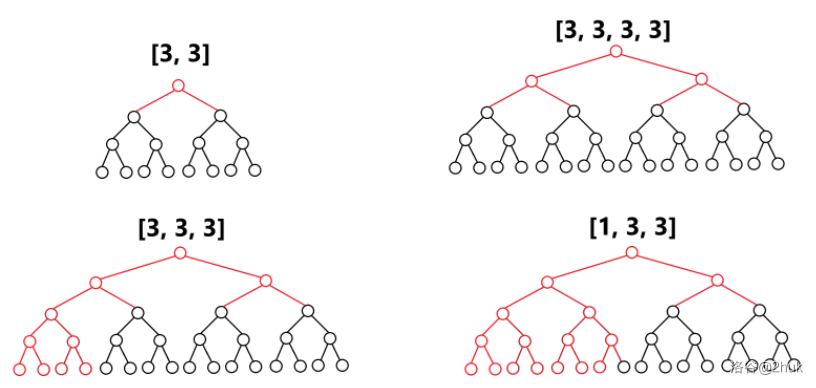

![](https://cdn.luogu.com.cn/upload/image_hosting/oz0jml3d.png)

---

着重分析一下 $[1,3,3]$。首先我想把 $1$ 跟别的对齐，就需要造一个深度为 $3$ 的满二叉树。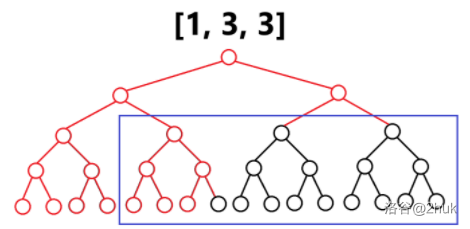

![](https://cdn.luogu.com.cn/upload/image_hosting/xa7254x9.png)

（实际上这里省了一步，应该先造深度为 $2$ 的，发现还不够，再造了 $3$。）

然后变成了 $[3, 3, 3]$ 的问题。直接连肯定不行，因为需要是二叉树。所以再造一个深度为 $3$ 的。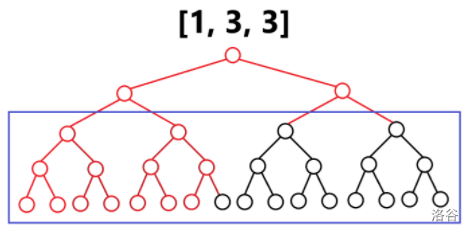

![](https://cdn.luogu.com.cn/upload/image_hosting/1tqcalwu.png)

然后变成了 $[3, 3, 3, 3]$ 的问题。把前两个和后两个分别合成深度为 $4$ 的。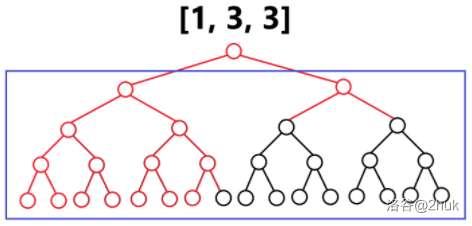

![](https://cdn.luogu.com.cn/upload/image_hosting/4o17ifak.png)

然后是 $[4, 4]$ 的问题。显然能合并成一个 $5$。结束了。

---

形式化的，这个过程是 $[1, 3, 3] \to [2, 3, 3] \to [3, 3, 3] \to [4, 4] \to [5]$。也就是每次把所有最小的数删掉（令最小的数是 $x$，有 $y$ 个），然后添加 $\lceil \frac y2 \rceil$ 个 $x+1$。重复这个过程直到只剩一个数。最后这个数就是 $f(u)$。

暴力代码是这样的：

```cpp
void dfs(int u) {
	f[u] = 0;
	
	if (g[u].empty()) {
		f[u] = 1;
		return;
	}
	
	if (g[u].size() == 1) {
		dfs(g[u][0]);
		f[u] = f[g[u][0]] + 1;
		return;
	}
	
	map<int, int> cnt;
	for (int v : g[u]) {
		dfs(v);
		cnt[f[v]] ++ ;
	}
	
	while (cnt.size() != 1 || (*cnt.begin()).second != 1) {
		int x = (*cnt.begin()).first;
		int y = (*cnt.begin()).second;
		cnt[x + 1] += (y + 1) / 2;
		cnt.erase(x);
	}
	
	f[u] = (*cnt.begin()).first;
}
```

直接这样交会 [TLE on test #62](https://codeforces.com/contest/2031/submission/292119672)。其实这样复杂度是错误的，因为求一个 DP 值的复杂度是 $f(v)$ 的值域，也就是 $\mathcal O(n)$。总复杂度是平方的。[hack generator](https://www.luogu.com.cn/paste/4wqoib1w)。

---

怎么优化？

仍然考虑这个例子 $[1, 3, 3]$。在最上面模拟时，我们跳过了 $[2, 3, 3]$ 这一步，而是直接到了 $[3, 3, 3]$。考虑实现这一点。

也就是我们考虑这一个 $1$ 最终会变成几个 $3$。更一般的，我们考虑 $x$ 个 $y$ 最终会变成几个 $y+k$（$k > 0$），且 $y,y+k$ 是原数组排好序后的相邻的两个数。

不难发现这个答案是从 $x$ 开始，执行 $k$ 次除以二上取整的答案。注意到当过程中 $x$ 变为 $1$ 后，最终结果一定是 $1$，此时可以直接退出。不难证明这样做最多只有 $\mathcal O(\log n)$ 次。

总复杂度 $\mathcal O(n \log n)$。常数挺大。

```cpp
#define tests
#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 10;

int n, fa[N];
vector<int> g[N];
int f[N];		// i 的子树，需要几层满二叉树

int work(int x, int y) {
	if (!x) return 0;
	if (y > 60) return 1;
	while (y -- ) x = (x + 1) / 2;
	return x;
}

void dfs(int u) {
	f[u] = 0;
	
	if (g[u].empty()) {
		f[u] = 1;
		return;
	}
	
	if (g[u].size() == 1) {
		dfs(g[u][0]);
		f[u] = f[g[u][0]] + 1;
		return;
	}
	
	map<int, int> cnt;
	for (int v : g[u]) {
		dfs(v);
		cnt[f[v]] ++ ;
	}
	
	vector<pair<int, int>> vec;
	for (auto e : cnt) vec.push_back(e);
	
	for (int i = 0; i + 1 < vec.size(); ++ i ) {
		vec[i + 1].second += work(vec[i].second, vec[i + 1].first - vec[i].first);
	}
	
	while (vec.back().second != 1) {
		vec.back().first ++ ;
		vec.back().second = (vec.back().second + 1) / 2;
	}
	
	f[u] = vec.back().first;
}

void solve() {
	cin >> n;
	
	for (int i = 1; i <= n; ++ i ) {
		g[i].clear();
	}
	
	for (int i = 2; i <= n; ++ i ) {
		cin >> fa[i];
		g[fa[i]].push_back(i);
	}
	
	dfs(1);
	
	cout << f[1] - 1 << '\n';
}

signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	int T = 1;
#ifdef tests
	cin >> T;
#endif
	while (T -- ) solve();
	return 0;
}
```

正在渲染内容...