ST表 - 洛谷保存站

## 壹.$\texttt{ST}$表是啥
$\texttt{ST}$表是一种数据结构，基于倍增思想，可以高效解决$\texttt{RMQ(range maximum/minimum query)}$问题（区间最值），在经过$O(nlog_2n)$的预处理后，可以实现在线$O(1)$查询区间$[l,r]$的 $\texttt{maximum/minimum}$。

## 贰.$\texttt{ST}$表示如何实现的
在 **壹** 中介绍过，$\texttt{ST}$表是基于倍增思想的，下面我们以求数组$a$的$\texttt{maximum}$为栗子：

---

定义：$st_{i,j}$表示从$i$开始长度为$2^j$的区间最大值，也就是$[i,i+2^j-1]$的$\texttt{maximum}$，显然，$st_{i,0}=a_i$。

---

随后，我们通过动态规划的方式预处理，一个长度为$2^j$的区间是由两个长度为$2^{j-1}$的区间组成的，所以得到
$$st(i,j)=max(st_{i,j−1},st_{i+2^ 
{j−1}
 ,j−1})$$
 
这是图解：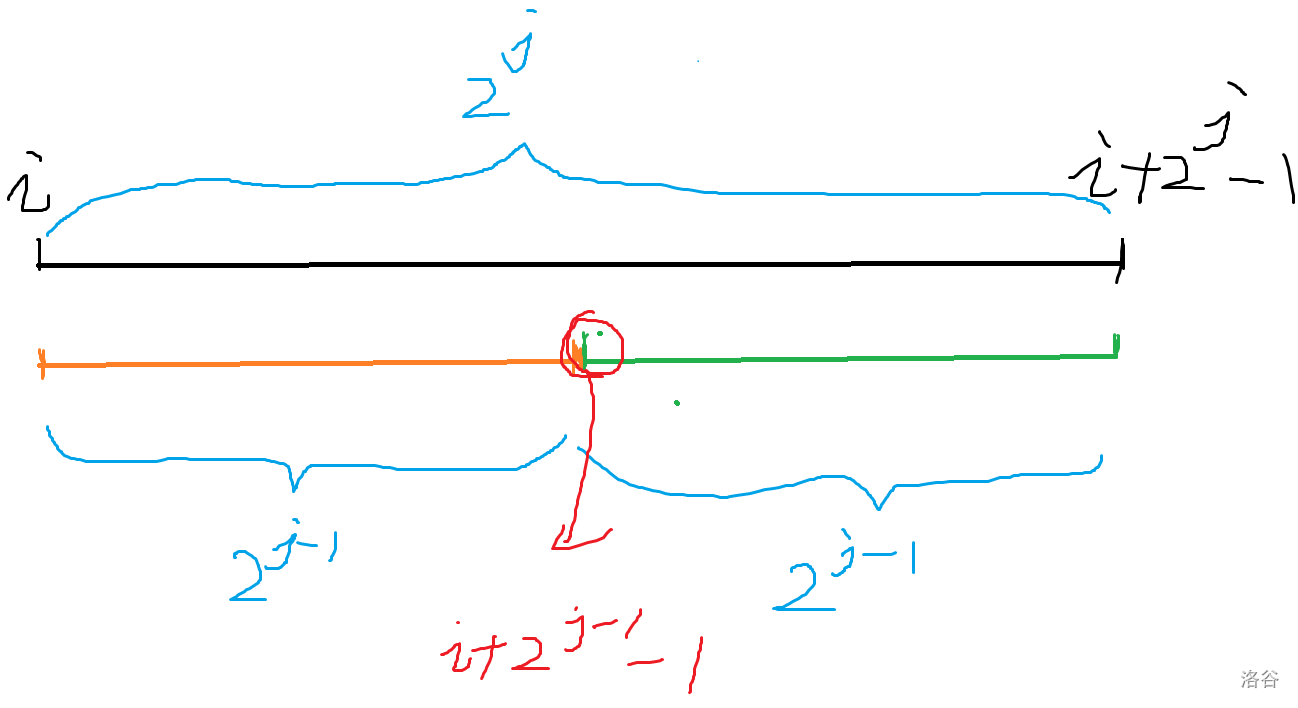
![](https://cdn.luogu.com.cn/upload/image_hosting/ecs6lhx2.png)

---

预处理完成了，那么该如何查询呢?  
对于区间$[l,r]$，我们要把它分成两个区间，然后这两个区间的$\texttt{maxn}$即为答案。

那么这两个区间该咋分呢，仔细想想，应该满足两个条件：  
1. 这两个区间的并不能超过原区间的左右界，否则就会有多的数进来比较。
2. 这两个区间可以有重叠部分，但必须完全覆盖原区间，做到可重复，不遗漏。

那么，我们就可以计区间长度为$len$，从$l$向右找长度为$2^{log_2len}$の区间，从$r$向左找长度为$2^{log_2len}$の区间，取$\texttt{max}$即可。

当然为了保证询问复杂度为$O(1)$，我们需要提前预处理出每个$log_2len$向下取整后的值。

## 叁.$\texttt{code}$

```cpp
#include <iostream>
#include <cmath>
using namespace std;

const int N = 100005;  // 数组最大长度
const int K = 20;      // 2^20足够覆盖1e5

int a[N];  // 原始数组
int st[K][N];  // ST表
int lg[N];  // log表

int main() {
    int n;
    cin >> n;
    
    // 读入数据
    for (int i = 0; i < n; ++i) {
        cin >> a[i];
        st[0][i] = a[i];
    }
    
    // 预处理log表
    lg[1] = 0;
    for (int i = 2; i <= n; ++i) {
        lg[i] = lg[i/2] + 1;
    }
    
    // 构建ST表
    int k_max = lg[n] + 1;
    for (int j = 1; j < k_max; ++j) {
        for (int i = 0; i + (1 << j) <= n; ++i) {
            st[j][i] = max(st[j-1][i], st[j-1][i + (1 << (j-1))]);
        }
    }
    
    // 查询示例
    int q;
    cin >> q;
    while (q--) {
        int l, r;
        cin >> l >> r;
        int len = r - l + 1;
        int k = lg[len];
        int res = max(st[k][l], st[k][r - (1 << k) + 1]);
        cout << res << endl;
    }
    
    return 0;
}

```

正在渲染内容...