题解：P9031 [COCI2022-2023#1] Iksevi

先考虑如何判断 $(x,y)$ 是否在直径为 $2r$ 的地毯的角上。

不难发现一个必要条件是 $r \mid x \land r \mid y$，即 $r \mid \gcd(x, y)$。

满足这个条件的 $(x, y)$ 在图上是这些：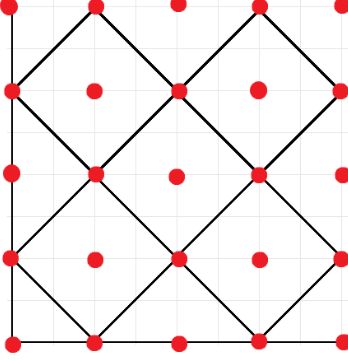

![](https://cdn.luogu.com.cn/upload/image_hosting/vw8oya22.png)

然后猜出充分条件是 $2r \nmid x+y$。重申一遍：

- $r \mid \gcd(x, y)$
- $2r \nmid x+y$

考察第二个条件。可以改写成：

- $2 \nmid x+y$ 或 $r \nmid (x+y)/2$。

于是可以对 $x+y$ 的奇偶性分类讨论。

- $x+y$ 是奇数：那么第二个条件相当于无效了。于是答案为 $D(\gcd(x,y))$。（$D(x)$ 表示 $x$ 的约数个数。）
- $x+y$ 是偶数：问题变成了求 $\gcd(x, y)$ 的约数和 $(x+y)/2$ 的约数的补集的交集的大小（有多少 $r$ 满足 $r \mid \gcd(x, y) \land r \nmid (x+y)/2$）。根据 **容斥原理**，答案为 $D(\gcd(x, y)) -D(\gcd(\gcd(x,y),(x+y)/2))$。原因如下：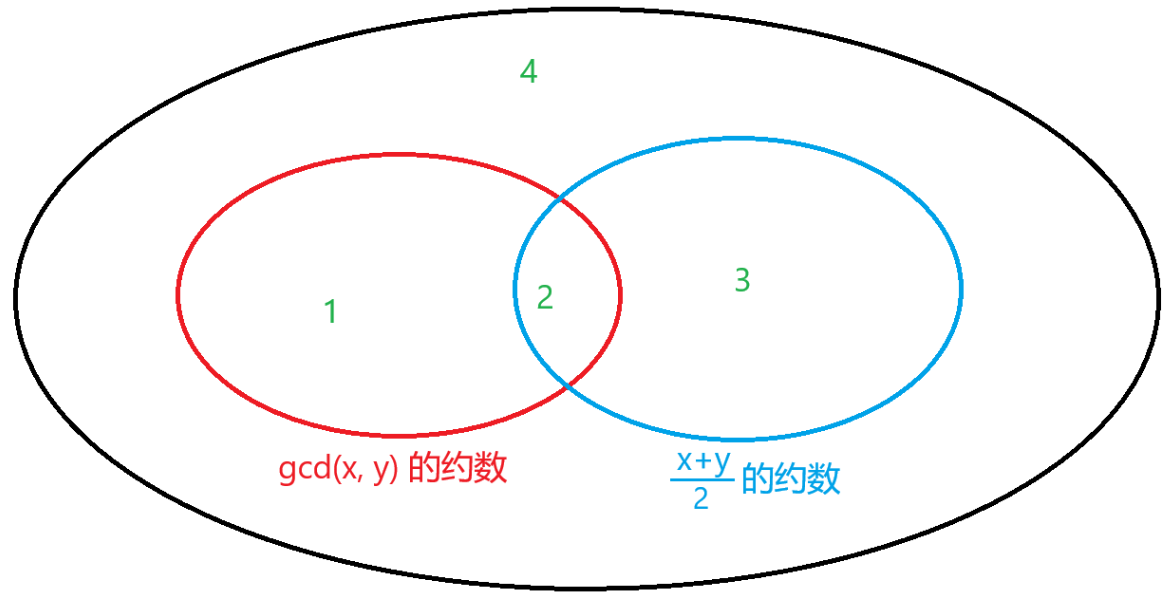

> ![](https://cdn.luogu.com.cn/upload/image_hosting/fpgqrle4.png)
> 
> $\gcd(x,y)$ 的约数是 $1,2$ 部分，非 $(x+y)/2$ 的约数是 $1,4$ 部分，它们的交是第 $1$ 部分，也就是 $\gcd(x,y)$ 的约数除去 $\gcd(\gcd(x,y),(x+y)/2)$ 的约数。

于是需要预处理 $1 \sim 10^7$ 的约数个数。

```cpp
// Problem: 
//     P9031 [COCI2022-2023#1] Iksevi
//   
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P9031
// Memory Limit: 512 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#define tests
#include <bits/stdc++.h>

using namespace std;

const int N = 1e7 + 10;

int D[N];

void solve() {
	int x, y;
	cin >> x >> y;
	if ((x + y) % 2) cout << D[__gcd(x, y)] << '\n';
	else cout << D[__gcd(x, y)] - D[__gcd(__gcd(x, y), x + y >> 1)] << '\n';
}

signed main() {
	for (int i = 1; i < N; ++ i )
		for (int j = i; j < N; j += i) D[j] ++ ;
	
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	int T = 1;
#ifdef tests
	cin >> T;
#endif
	while (T -- ) solve();
	return 0;
}
```

正在渲染内容...