主页
搜索
最近更新
数据统计
申请密钥
批量保存
开发版网站(新前端)
系统公告
1
/
1
请查看完所有公告
today I'm beat becase of DP Competition
最后更新于 2025-08-27 17:44:08
作者
Tangziming625127
分类
个人记录
复制 Markdown
查看原文
转到新前端
删除文章
更新内容
今日总结(8/26) # T2 题目: 在一段序列中选最多的数 组成一个所有数互为倍数的集合 考虑倍数关系,如果一个数字 c 能被 b 整除, b 能被 a 整除,那么 c 一定可以被 a 整除。 那就可以考虑重复的情况 因为里面有很多数是原有的数里的倍数故可以考虑为唯一分解定理比如 6 答案的来源实际上是 2 和 3 , 那么我们在处理后面 6 答案的时候可以只用 2 和 3 。 也可以单纯的素数标记 注意:t2也是有一个情况, 就是数字的个数和数字大小貌似能发现,数字如果离散化之后,也就是 n 的数量, 枚举范围统计的时候,其实桶里面有很多数据是空的 这时直接跳过 代码: ```cpp #include<bits/stdc++.h> using namespace std; const int maxn=1e7+7; int n,x; int dp[maxn],res,cnt[maxn]; int main(){ cin >> n; int maxx = 0; for(int i=1;i<=n;i++){ cin >> x; cnt[x]++; maxx = max(maxx,x); } for(int i=1;i<=maxx;i++){ if(cnt[i]){ dp[i]+=cnt[i]; for(int j=2*i;j<=maxx;j+=i){ dp[j]=max(dp[j],dp[i]); } } res=max(dp[i],res); } cout << res << '\n'; return 0; } ``` # T3 题意简化:给定一个长度为 $n$ 的数组,求长度为 $n-m$ 的不同子序列个数。 由于m数只是要删不考虑什么数 故我们可以设状态为 dp[i][j] 表示从前面i个数字之中删除j个数字的方案的数量 答案就为dp[n][m] % mod 转移方程: dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] 可是处理dp过程之中存在重复子问题交叉的情况 比如这里举例1 3 1 删除前面的1 3 和 后面的 3 1 本题考察的是剩余情况的答案种类,所以在此处的考虑这样是重复的 故要考虑去重 假设目前相等那么从某个位置x到达上一个相等的数字的位置pre[x]必须删除才会重复 此时考虑的情况就是前面剩余的pre[x] - 1个数字 只能允许删除j -i+pre[x]个数字 也就是dp[pre[x] - 1][j - i + pre[x]] 初始化: dp[i][0] = 1; dp[i][i] = 1; 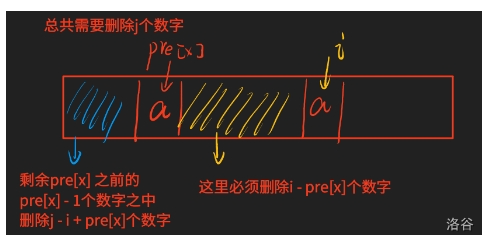 ```cpp #include<bits/stdc++.h> using namespace std; const int mod = 1e9+7; const int maxn = 1e5+7; map<int,int>dp[maxn]; int pre[maxn]; int ton[maxn]; int n,m,k; int a[maxn]; int main(){ while(cin >> n >> m >> k){ for(int i=0;i<=n;i++){ dp[i].clear(); } memset(pre,0,sizeof(pre)); memset(ton,0,sizeof ton); for(int i=0;i<=n;i++){ dp[i][0]=dp[i][i]=1; } for(int i=1;i<=n;i++){ cin >> a[i]; pre[i]=ton[a[i]]; ton[a[i]]=i; } for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ dp[i][j] = (dp[i-1][j-1] + dp[i-1][j])%mod; int pos = pre[i]; if(i-pos <= j and pos - 1 >= 0){ dp[i][j] = (dp[i][j] - dp[pos-1][j-(i-pos)] + mod)% mod; } } } cout << dp[n][m] % mod << '\n'; } return 0; } ``` # T4 题意简化: 给定n片区域的芒果的位置以及对应的的成熟时间 小梦可以进行广播,每次广播给定一个距离x,收割di<x以内的所有成熟的芒果,1s只能一次广播 要求 x 的最小总和。 对于 100% 的数据范围 我们可以将时间看作区间范围,作为 x 轴的变换方向,另外距离当作 y 轴,此时将问题转换为区间内选多条直线覆盖所有的区间 一条直线覆盖多个区间,取区间的最高的距离当作答案的一部分,求解距离和的最小值。 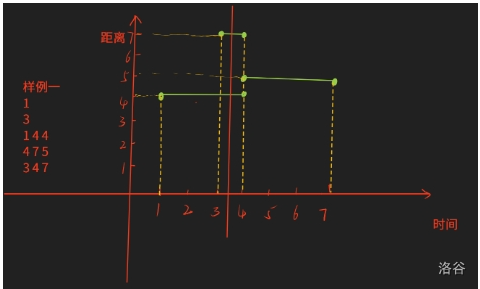 那不就是在每段按照右端点从小到大排序,然后进行从右往左进行选择, 但是可以被hack  因为这时可能会有后面的选择覆盖前面的 导致前面的更优秀 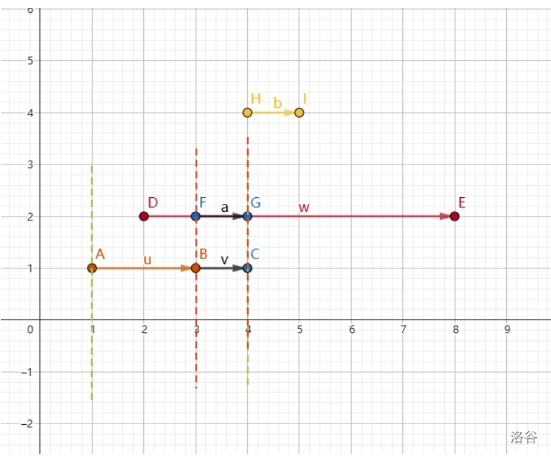 如图中可以将红色虚线移动到左边的绿色虚线部分 将时间看成横向的 x 坐标, 距离看成竖向的 y 坐标之后 发现线段整体是一个区间 考虑区间Dp的做法 dp[l][r]表示区间范围$[l,r]$ 之内覆盖所有线段的距离最小值 此时因为时间范围过大,通过离散化的形式,将时间区间转换为600个离散化单位,最终离散化的区间从$[1,10000]$转换到$[1,tot]$ 答案即为dp[1][tot]; 难点主要为转移部分 先写出状态转移 dp[l][r] = dp[l][m - 1] + dp[m + 1][r] + d, 其中d是区间[l, r] 内完全被包含的线段的最高点 如下图,这里画的竖线表示这里派出了员工,采摘距离最远的 4,黄色线段,顺便将下面的暗红色线段覆盖了 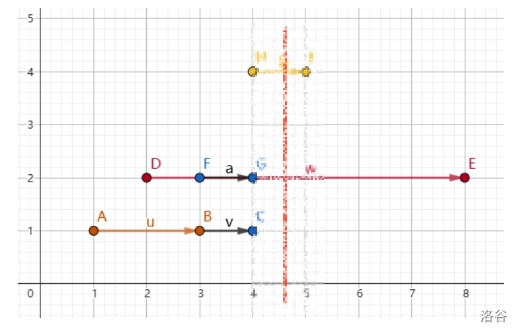 最高点所在的线段的选取,一定会影响它顺便可以覆盖到的答案。 此时我们的答案之和左边区间的答案和右边区间的答案有关, 就是每次选一条线 算左右边的贡献即可 但是这里不能重复计算,所以我们制定一个规则,参与 dp[l][r] 答案计算的区间,一定是能够完全被 [l,r] 范围包含的 如图: 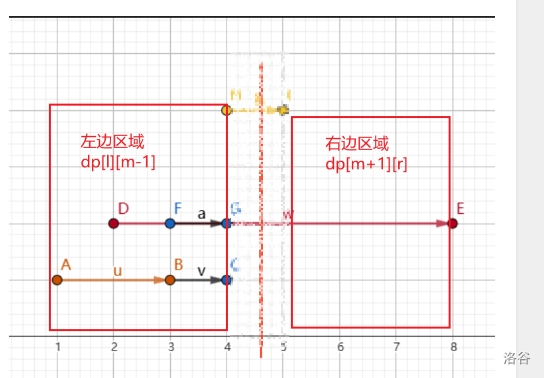 模糊的就不用考虑 因为他们引进被覆盖过了 当你选到后面的时候 就不用考虑前面的了 因为已经处理过了  所以就一定是由小区间转换为大区间 达到最大时 再考虑最高点的影响 所以这一段一段合并后就可以得到总距离 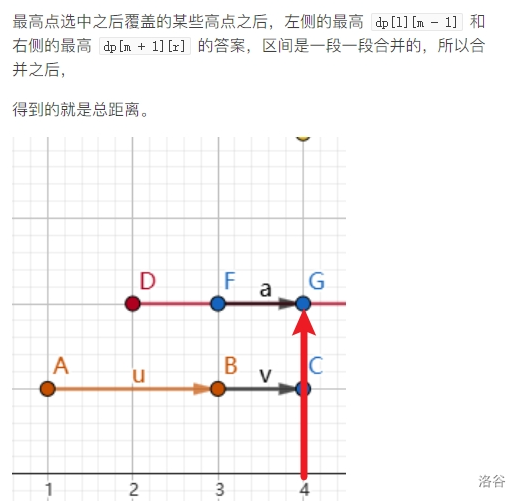 ```cpp #include<bits/stdc++.h> using namespace std; const int maxn=607; const int maxm=1e4+7; int dp[maxn][maxn]; int id[maxm*10]; bool vis[maxm*10]; struct node{ int a,b,d; }G[maxn]; int main(){ int T; cin >> T; while(T--){ int n; cin >> n; memset(vis,0,sizeof vis); memset(dp,0,sizeof(dp)); for(int i=1;i<=n;i++){ cin >> G[i].a >> G[i].b >> G[i].d; vis[G[i].a] = 1; vis[G[i].b] = 1; } int tot = 0; for(int i=1;i<=10001;i++){ if(vis[i]){ id[i]=++tot; } } for(int i=1;i<=n;i++){ G[i].a = id[G[i].a]; G[i].b = id[G[i].b]; } for(int len = 1;len <= tot;len++){ for(int i = 1;i+len-1 <= tot;i++){ int l=i,r=i+len-1; int pos = -1; int d=0; for(int j=1;j<=n;j++){ if(G[j].a >= l and G[j].b <= r){ if(G[j].d > d){ d = G[j].d; pos = j; } } } if(pos == -1){ continue; } dp[l][r] = 2e9; for(int j=G[pos].a;j<=G[pos].b;j++){ dp[l][r]=min(dp[l][r],dp[l][j-1]+dp[j+1][r]+d); } } } cout << dp[1][tot] << '\n'; } return 0; } ```
正在渲染内容...
点赞
0
收藏
0