2-SAT 求具体方案 - 洛谷保存站

现在我们已经把边连完了，并且是合法的。现在我们要求出一组具体的方案。

我们的规则是，对于一组对立的变量，我们要选拓扑序靠后的（即Tarjan更靠近叶子的）。

## 1. 反证法的假设

+ 对变量 $x_i$，存在 $(i,p)$，和 $(i,p\oplus1)$，其中 $f(i,p)<f(i,p\oplus1)$，按照规则我们应该选 $(i,p\oplus1)$。

+ 对变量 $x_j$，存在 $(j,q)$，和 $(j,q\oplus1)$，其中 $f(j,q)>f(j,q\oplus1)$，按照规则我们应该选 $(j,q)$。

+ **冲突条件**：存在路径 $P1:(j,q)\rightarrow (i,p)$ 则产生矛盾。因为选 $(j,q)$ 就必须要选 $(i,p)$，但按照规则，我们选了 $(i,p\oplus1)$，所以不能选 $(i,p)$。

## 2. 利用对称性推导路径

先介绍两个引理：

**引理 1** 
> 若存在边 $(i,p)\rightarrow(j,q)$，则一定存在边 $(j,q\oplus1)\rightarrow(i,p\oplus1)$。

证明：后者是前者的逆否条件。如果没有选 $(j,q)$，则一定没有选 $(i,p)$。

**引理 2** 
> 若存在路径 $(i,p)\rightarrow(j,q)$，则一定存在路径 $(j,q\oplus1)\rightarrow(i,p\oplus1)$。

证明：对路径上每一条边使用引理 1。

---
对 $P1$ 使用引理 2，得到**反向路径** $P2:(i,p\oplus1)\rightarrow(j,q\oplus1)$。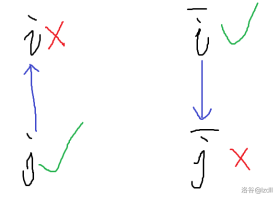

![graph](https://cdn.luogu.com.cn/upload/image_hosting/eawvhvtp.png?x-oss-process=image/resize,m_lfit,h_200)

图片中左侧的蓝边为 $P1$，右侧的蓝边为 $P2$。选了 $(j,q)$ 和 $(i,p\oplus1)$。

## 3. 推出矛盾
为了更清晰，下面使用 $i$，$\overline i$ 分别表示 $(i,p)$ 和 $(i,p\oplus1)$。$j$，$\overline j$ 分别表示 $(j,q)$ 和 $(j,q\oplus1)$

首先根据假设，有：

$$\left\{\begin{matrix}
  &  i<\overline i&&(1)\\
  &  \overline j<j&&(2)
\end{matrix}\right.$$

然后，根据我们连的蓝色的边，又能得到：

$$\left\{\begin{matrix}
  &  j<i&&(3)\\
  &  \overline i<j&&(4)
\end{matrix}\right.$$

其中，$(1),(3),(4)$ 三个式子会推出矛盾。

## 4. 矛盾的意义：规则必然合法

反证法中，“假设按规则选,会冲突”推导出逻辑矛盾，说明**假设不成立**。因此：

**对每个变量，选择其所在强连通分量拓扑序更大的节点，必然无冲突，一定能构造合法解。**

然后 Tarjan 里边，所属的强联通分量编号恰好是**逆拓扑序**，也就是说，越靠近叶子，编号越小，拓扑序越大。

所以我们代码里面直接这么写：

其中 $bel[i]$ 表示所属的强连通分量编号，$val[i]=0/1$ 表示选 $0$ 还是选 $1$。
```cpp
	for(int i=1;i<=n;++i){
		val[i]=bel[i]>bel[i+n];
	}
    //哪个大就不选哪个
	for(int i=1;i<=n;++i){
		cout<<val[i]<<" ";
	}
```

正在渲染内容...