题解：CF1025D Recovering BST

**题目保证了输入 $a_i$ 递增。**

因为是二叉排序树，所以**树上每颗子树都能对应序列上一个区间**。或者说，这棵树的中序遍历就是给定的序列。

有个性质：$[l, r]$ 对应的子树里，$l$ 是最小值，$r$ 是最大值；且从根开始一直向左走最后到达的点是 $l$，一直向右走最后到达的点是 $r$。如果你学过笛卡尔树理解这些是容易的。

考虑区间 DP。设 $f(l, r, k)$ 表示能否将 $[l, r]$ 内的值构造一棵合法的二叉排序树，且其根为 $k$。转移考虑枚举 $[l, k - 1]$ 的根节点和 $[k + 1, r]$ 的根节点。对于答案，判断是否存在 $k$ 使得 $f(1, n, k)$ 为真即可。

时间复杂度 $\mathcal O(n^4)$，过不了。

注意到 $f(l, r, k) = f(l, k, k) \land f(k,r,k)$。所以你可以只记录 $f(l, r, 0/1)$ 表示 $k$ 是左端点还是右端点。状态数做到 $\mathcal O(n^2)$。

考虑转移。我们以 $f(l, r, 0)$，即以 $l$ 作为根为例。

考虑枚举 $r$ 的父亲 $k$。这里需要满足 $\gcd(a_r, a_k) \ne 1$。

根据性质，你从 $l$ 出发，一直往右走，最后到达的点一定需要是 $r$。所以 $r$ 的父亲是 $k$ 就意味着 $r$ 是 $k$ 的**右儿子**。

因为你走到头了，所以 $r$ 必须没有右子树。这时你想到了 $f(?,r,1)$ 的定义。但是这个 $?$ 应该是什么呢？

再根据性质，$?$ 是从根（$r$）出发，一直向左走最后到达的点。这个点是否确定？

确定。从 $k$ 开始，先向右走（到达 $r$），再一直向左走直到走不动，此时所在的点是 $k$ 的后继。而 $k$ 的后继是 $k + 1$。所以这个 $?$ 是 $k + 1$。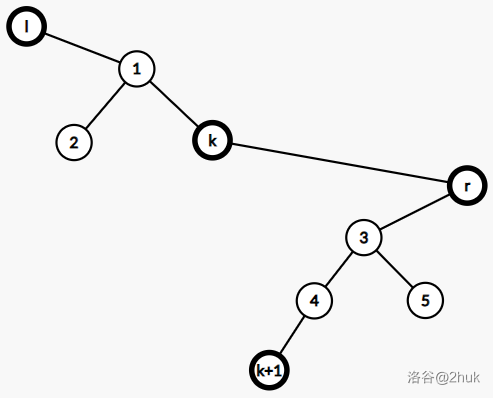

![](https://cdn.luogu.com.cn/upload/image_hosting/wkancudd.png)

而除去 $r$ 的子树外，剩下的子树对应区间 $[l, k]$，且以 $l$ 为根。所以 $k$ 合法当且仅当：

$$
f(l,k,0) \land f(k+1,r,1)
$$

总转移是（懒得打 $\LaTeX$ 了，看代码吧）：

```cpp
for (int k = l; k < r; ++ k )
	if (f[l][k][0] && f[k + 1][r][1]) {
		if（gcd(a[k], a[r]) > 1) f[l][r][0] = true;
		if (gcd(a[k + 1], a[l]) > 1) f[l][r][1] = true;
	}
```

判断答案从原来的 $f(1, n, k)$ 变成了 $f(1, k, 1) \land f(k, r, 0)$。

完整 AC 代码：

```cpp
#include <bits/stdc++.h>

using namespace std;

const int N = 710 + 10;

int n, a[N];
bool f[N][N][2];
int g[N][N];

signed main() {
	cin >> n;
	for (int i = 1; i <= n; ++ i ) {
		cin >> a[i];
		f[i][i][0] = f[i][i][1] = true;
	}
	
	for (int i = 1; i <= n; ++ i )
		for (int j = 1; j <= n; ++ j )
			g[i][j] = __gcd(a[i], a[j]);
	
	for (int len = 2; len <= n; ++ len )
		for (int l = 1, r = len; r <= n; ++ l, ++ r )
			for (int k = l; k < r; ++ k )
				if (f[l][k][0] && f[k + 1][r][1]) {
					if (g[k][r] > 1) f[l][r][0] = true;
					if (g[k + 1][l] > 1) f[l][r][1] = true;
				}
	
	for (int i = 1; i <= n; ++ i )
		if (f[1][i][1] && f[i][n][0]) {
			puts("Yes");
			return 0;
		}
	
	puts("No");
	return 0;
}
```

这个题卡了求 $\gcd$ 的 $\log$，所以我们用 $\mathcal O(n^2 \log V)$ 预处理每个对的 $\gcd$。总复杂度是 $\mathcal O(n^3)$ 的。

正在渲染内容...